10月9日更新的2018年河北公务员考试每日一练是数量关系题，多做公务员考试模拟题练习不仅有利于掌握考点，而且能够帮助保持题感，潜移默化中熟悉命题规律，提高公务员考试做题准确率。

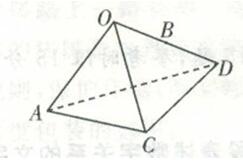
　　1．一只小虫从棱长为2的正三棱锥（如图）中的A点爬到B点（为所在线段的中点），且小虫只在面OAC和面OCD中移动。问该小虫爬过的最短路程为（  ）

　　A．            B．               C．           D．3

　　2．甲、乙、丙、丁四支足球队展开单循环比赛，任意两队之间都要比赛1场，已知甲队已比赛了3场，乙队已比赛了2场，丙队已比赛了1场，则丁队已比赛了几场（  ）

　　A．3     B．2     C．1     D．0

　　3．小明所在的高二年级共10个班300人，每个班级人数都不相同。若人数第4多的班级有31人，则人数最多的班级至少有多少人（  ）

　　A．37     B．36     C．35     D．34

　　4．一个正十二面体随意翻动，每次翻动朝上一面的颜色与翻动前都不同，那么这个正十二面体的颜色至少有几种（  ）

　　A．3     B．4     C．5     D．6

　　5．朝阳公园拟定在一个400米的环形跑道两侧每隔五米种植1棵香樟树（内外环周长差以及树桩直径长度忽略不计），并把这项植树任务平均分配给公园的4个工人。但1个工人正准备休假，为了使该工人正常休假，且其他工人的工作量减少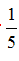，则还需要外聘几个工人（  ）

　　A．1      B．2      C．3      D．4

　　【下面是参考答案与解析。如果你认为题目或解析有误，可点这里给我们纠错。】

　　1．【解析】B。将面OAC和面OCD在同一平面内铺开，可得边长为2的菱形OACD（如下图），小虫爬过的最短路程应为线段AB的长度。因为△OCD为等边三角形，又B点为OD中点，因此∠OCB=30°，∠ACB =∠ACO+∠OCB=90°，则△ACB为直角三角形。由勾股定理可知，BC=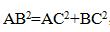，，所以。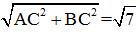

　　2．【解析】B。一场比赛有两支足球队参加，则所有队伍进行的比赛场数之和必为偶数，排除A、C两项。总共有四支足球队单循环比赛，甲队已比赛了3场，则必与丁队进行过一场比赛，排除D项。

　　本题也可用常规方法分析求解。甲、乙、丙、丁四支足球队，甲队已比赛了3场，说明甲队与乙、丙、丁队各赛了1场。丙队只比赛了1场，说明丙队只和甲队比赛了1场。乙队已比赛了2场，只能是同甲队、丁队各赛1场。因此丁队共进行了同甲队、乙队的2场比赛，B项正确。

　　3．【解析】B。根据最不利原则，要使人数最多的班级人数尽量少，则其他班级人数应尽可能地多。设人数最多的班级最少有x人，人数排名第二的班级有（x-1）人，人数排名第三的班级有（x-a）人（a＞1），则其他班级人数如下表所示：

　　由上表可知，人数排名4~10的班级总人数为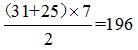，则排名前3的班级总人数为104。根据题意列方程x+（x-1）+（x-a）=104，解得x=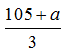。因为a是整数且a＞1，所以当a取3时，方程有最小整数解x=36。

　　4．【解析】B。正十二面体每个面与五个面相邻，令朝上一面颜色为A，与其相邻的面颜色依次为B、C、D、B、C，而另六个面中，令朝下一面颜色为B，此时与其相邻的五个面均能与各自的相邻面区别开颜色。因此正十二面体最少需要4种颜色才能使朝上一面的颜色每次翻动后都与之前不同。本题选B。

　　实际上，如果熟悉著名的“四色定理”，本题可快速作答。四色定理：每个平面（或球面）地图都可以用不多于四种颜色来染色，而且没有两个邻接的区域颜色相同。题干中正12面体可看作一个球面，根据“四色定理”，使用不多于四种颜色，就可以使相邻两个面颜色不同，因此C、D两项可以排除。正十二面体每个面与5个面相邻，这5个面首尾相连，5是奇数，则至少需要3种颜色才能使这5个面之间任意相邻两个面颜色不同，而这5个面围住的1个面的颜色与这5个面都不相同。综上分析，只考虑正12面体的6个面时，就需要至少4种颜色才能满足要求，排除A项。

　　5．【解析】B。400米跑道每隔五米种1棵香樟树，两侧都种，则共种植香樟树400÷5×2=160（棵），减少工作量后，每人的工作量为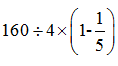=32（棵），共需要160÷32=5（人），有一个工人正在休假，所以需要再外聘2个工人。

　　更多试题练习：2018年公务员考试行测标准预测卷