1.用一根绳子测量一口枯井的深度，如果绳子对折去量就多出4米，三折去量就多出1米，则该井的深度是（  ）

　　A.6米      B.5米      C.4米      D.3米

　　2.乙、丙三人同去商城购物，甲花钱的等于乙花钱的，乙花钱的等于丙花钱的，结果丙比甲多花93元，则三人一共花的钱是（  ）

　　A.432元      B.422元      C.429元      D.430元

　　3.现需要购买两种调料加工成一种新调料，两种调料的价格分别为20元/千克、30元/千克，如果购买这两种调料所花钱一样多，则每千克新调料的成本是（  ）

　　A.23元      B.25元      C.24元      D.29元

　　4.一个公比为2的等比数列，第n项与前n－1项和的差等于3，则此数列的前四项之和是（  ）

　　A.54      B.45      C.42      D.36

　　6.有100克溶液，第一次加入20克水，溶液的浓度变成50%；第二次再加入80克浓度为40%的同种溶液，则溶液的浓度变为（  ）

　　A.45%      B.47%      C.48%      D.46%

 

　    河北公务员考试网（http://www.hebeigwy.org/）解析　题目或解析有误，我要纠错。

 

　　1.【解析】B。利用代入排除法求解。代入A项，根据“绳子对折去量就多出4米”求得绳长为（6+4）×2=20（米）；根据“三折去量就多出1米”求得绳长为（6+1）×3=21（米），两者不一致，排除。

　　代入B项，根据第一个条件求得的绳长为（5+4）×2=18（米），根据第二个条件求得的绳长为（5+1）×3=18（米），两者一致，当选。

　　2.【解析】C。根据已知条件可得，甲、乙花钱之比为︰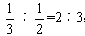，乙、丙花钱之比为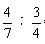=16︰21，则甲、乙、丙花钱之比为32︰48︰63，那么三人花的总钱数一定能被32+48+63=143整除。验证发现，只有C项能被143整除，当选。

　　3.【解析】C。由“购买这两种调料所花钱一样多”，不妨设都花了60元（取20和30的最小公倍数），这样问题便迎刃而解了。设购买两种调料都花了60元，则分别买了3千克和2千克，那么每千克新调料的成本为

　　4.【解析】B。根据“第n项与前n－1项和的差等于3”可得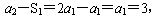，则该数列前四项分别为3，6，12，24，前四项和为3＋6＋12＋24＝45，B项正确。

　　5.【解析】D。本题属于题型Ⅰ，已知第一次加入水后的溶液质量A=120，浓度a=50%，第二次加入的溶液质量B=80，浓度b=40%，求混合后的浓度r，利用十字交叉法公式求解。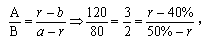解得r=46%，D项正确。