图形推理中的空间重构类题目，虽然其考查形式比较单一，一般都是折纸盒或拆纸盒的题目，但是由于其考查过程中纸盒形状的多样性、纸盒各个面上图形变化的灵活性以及内外表面变化的随意性，使其对考生而言“高深莫测”。其实，空间重构着重考察的是考生的空间思维能力，但是绝大多数考生的空间思维能力却并不突出，因此，要想彻底解决这个“后顾之忧”，河北公务员考试网（www.hebeigwy.org）为最优化的方法便是将其“平面化”--这是一个基本的解题思路。而要将其“平面化”，方法有两个：时针法和公共顶点法，如能将这两个方法掌握，则在解此类题目的过程中便无往而不利了。下面分别介绍一下这两种方法：

　　一、时针法

　　时针法是较为简单的一种方法，无非是以立体图形中相邻的三个面为基准，分别去选项中找寻这三个面，并按照同样的顺序画时针。然而并非任意三个面都可以画时针，在六面体中，能够画时针的三个面必须满足以下两个条件：(1)画时针的三个面必须不存在平行面;(2)画时针的时候必须保证这三个面至少两对两两有交点。二者缺一不可。如在下图中，两个平面图中1、2、3三个面都不平行，这满足了画时针的第一个条件;第一个图形中1、2两个面有交点，即两个红点，2、3两个面也有交点，即一个蓝点，第二个图形中1、2两个面的交点为a、b，1、3两个面的交点为b、c，2、3两个面的交点为b，第一个图形中两对面两两有交点，第二个图形中三对面都两两有交点，所以满足画时针的第二个条件，很明显，这两个图是可以直接画时针的。

　　但是，在有些空间重构类的题目中，是并不满足直接画时针的条件的。如：下图中的1点、3点、6点三个面，虽然三个面都不平行，但是很明显只有1点、3点之间有公共点，但是6点和它们并没有公共点，所以不满足画时针的条件(2)，此时要移动，根据平行面来移动，6点和2点平行，所以可以将6点移动到红字标出的1和2的位置，无论是1的位置还是2的位置都可以直接画时针了。

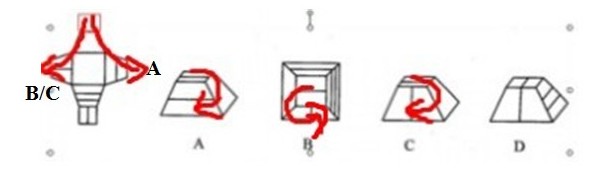
　　另外，在非正六面体中，时针法也完全适用，而且不论是内表面还是外表面,因为在平面图形中，内外皆可。如下题。A选项中的三个面在原图中找到后，发现不满足画时针的第2个条件，所以将类似立体容器盖子的最小正方形移到了上方，右边的逆时针为A选项在平面中的时针，与A立体图中的顺时针不一致，所以A错，同理可知C对。

　　下图给定的是纸盒的外表面，下面哪一项能由它折叠而成?

　　二、公共顶点法

　　此处的知识点有三条：(1)互相垂直的两条边(必须是长度一样的边)的端点是公共顶点;(2)对面/平行面之间不可能有公共顶点;(3)相交于同一个公共顶点下的三个面，其面上的图形必须与公共顶点的位置关系保持不变。

　　第(1)点有老师教研过，此处不再赘述，即下图中三个红点、三个蓝点折成立体图形后会是同一个公共顶点。第(2)点理解起来容易，但用起来难度较大。如何来用，如下图：两个粉色的点a、b是公共顶点。原因如下：a在1面和3面上就不可在1面和3面的平行面上即5和6面，而1、3、4的公共点也很显然，所以相交于a点的另一个面肯定是2面，而2面上的红点不可能，2面下方的两个点因为在6面上，自然也不能在其平行面3面上，所以也排除，只能是b点。

　　第(3)点用起来较简单，也比较常用，但要基于(1)和(2)两点即在找到公共顶点的情况下。如下面例题：

　　其中红点是A选项中的公共顶点，原图中1面上的斜线未经过公共点，而A选项经过了，所以错了;黑点是B选项中的公共顶点。原图中2面上的斜线未经过公共顶点，但B选项经过了，所以错了;C选项用公共顶点无法直接看出，可以用时针法排除，但要确定C选项中2、3这两个面也是有一定难度的，完全可以按照公共顶点，发现3面中红色线段标示的地方，相应的找到2和3面，直接用时针就可以。

　　行测更多解题思路和解题技巧，可参看2013年公务员考试技巧手册。