年龄问题是指研究两人或者多人之间的年龄变化和关系的问题。行测考试中常常涉及两人或者多人年龄之间的倍数关系。常见的考查方式为：今年小宁8岁，妈妈32岁，那么再过多少年妈妈的岁数是小宁的2倍？下面，专家就为考生讲解如何巧妙解答年龄问题。

　　年龄问题重要原则为：①任何两人年龄差不变；②任何两人年龄之间的倍数关系是变化的；③每过一年，所有的人都长了一岁。

　　上例中，今年小宁比妈妈小32-8=24岁，那么小宁与妈妈的年龄差永远为24岁。

　　当小宁从8岁长到12岁时，妈妈也长4岁，变为32+4=36岁。两人年龄的倍数由32÷8=4倍，变化到36÷12=3倍。

　　知识点一：如何解年龄问题

　　解决年龄问题的关键在于“年龄差不变”。一般说来，解决年龄问题需要从表示年龄间关系的条件入手理解数量关系，必要时可借助线段图和表格进行分析。主要的思考方式如下：

　　由差倍问题公式可得，小宁年龄为24÷（2-1）=24岁，即小宁24岁时，妈妈的年龄等于小宁的2倍，因此再过24-8=16年。

　　（2）因为行测考试中，数学运算均为选择题，对于表述直接的年龄问题，没有解题思路，或者计算比较繁琐时，可采用代入排除法。

　　例题1： 姐姐今年13岁，弟弟今年9岁，当姐弟俩岁数和是40岁时，姐姐多少岁？

　　A．22 B．34 C．36 D．43

　　解析：“此题答案为A。两人年龄差为13-9=4岁，用线段图显示数量关系，如下图所示：

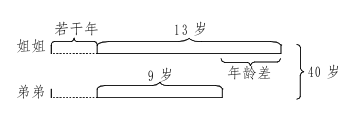
　　由图可知，如果从40岁中减去姐弟年龄的差，再除以2就得到弟弟的年龄，进而可求出姐姐的年龄，这相当于一个和差问题。

　　根据和差公式：弟弟的年龄为（40-4）÷2=18岁，则姐姐的年龄为18+4=22岁。

　　知识点二：多人之间的年龄问题

　　多人之间的年龄问题在行测考试中出现的频率略有增加，它主要考查多个人之间的年龄关系变化。解决此类题目的重点为规律③：每过一年，所有的人都长了一岁。

　　例题2： 父亲与两个儿子的年龄和为84岁，12年后父亲的年龄等于两个儿子的年龄之和，请问父亲现在多少岁？

　　A．24 B．36 C．48 D．60

　　解析：此题答案为C。12年后，父亲与两个儿子的年龄和应该是84+12×3=120岁，将父亲12年后的年龄看做1倍，那么12年后父亲的年龄为120÷2=60岁，现在的年龄为60-12=48岁。

　　例题3： 甲、乙、丙、丁四人今年的年龄分别是32、24、22、18岁，那么多少年前甲乙的年龄和恰好是丙丁年龄和的2倍？

　　A．15 B．14 C．12 D．10

　　解析：此题答案为C。画出线段图，如下图所示。

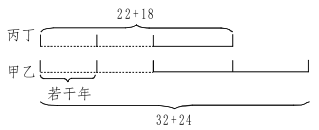
　　可知，（32+24）－（22+18）=16为甲乙年龄和与丙丁年龄和之差。

　　当甲乙的年龄和恰好是丙丁年龄和的2倍时，设丙丁年龄和为1倍，则甲乙年龄和为2倍，则1倍为16÷（2-1）=16，即丙丁当时的年龄和为16岁。

　　增加的年龄和为22+18-16，因此过了（22+18-16）÷2=12年。

　　知识点三：三等分结论

　　例题4： 甲对乙说：“当我的岁数是你现在的岁数时，你才5岁。”乙对甲说：“当我的岁数是你现在的岁数时，你将50岁。”那么，甲现在（ ）岁，乙现在（ ）岁。

　　解析：35、20。根据题意画出示意图，如下图所示：

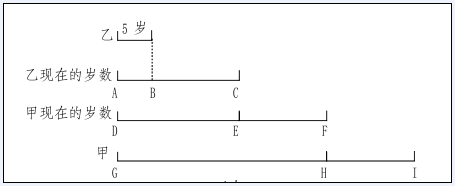
　　当乙5岁时，甲的年龄等于乙现在的岁数，用线段AC表示，可知甲、乙二人年龄差等于线段BC；

　　甲、乙现在的岁数差等于EF，当乙的岁数等于甲现在的岁数（用线段DF表示），甲将50岁（用线段GI表示），此时二人年龄差等于线段HI。

　　因为年龄差是不变的量，所以BC=EF=HI。

　　根据图示，GI=5+BC+EF+HI=5+3BC，所以甲乙二人的年龄差为：（50-5）÷3=15岁，乙现在的岁数是15+5=20岁。甲现在的岁数是20+15=35岁。

　　知识点四：年龄推理题

　　年龄推理题在行测考试中出现较少，它需要考生通过寻求年龄间的特殊情况来得到突破口，从而最终得出答案。

　　常见的特殊情况为：经过了N年，所有人增长的岁数和不是N的倍数，这说明N年前有人没有出生，从而可直接求出该人的年龄。

　　例题5： 小芬家由小芬和她的父母组成，小芬的父亲比母亲大4岁，今年全家年龄的和是72岁，10年前这一家全家年龄的和是44岁。今年父亲多少岁？

　　A．33 B．34 C．35 D．36

　　解析：此题答案为B。一家人的年龄和今年与10年前比较增加了72-44=28岁，而如果按照三人计算10年后应增加10×3=30岁，只能是小芬少了2岁，即小芬8年前出生，今年是8岁，今年父亲是（72-8+4）÷2=34岁。

      行测更多解题思路和解题技巧，可参看2012年公务员考试技巧手册。